Interval PLS (IPLS) for Variable Selection
Introduction
Similar to Genetic Algorithms for Variable Selection (GA), Interval PLS (IPLS) selects a subset of variables which will give superior prediction compared to using all the variables in a data set. Unlike the GA, IPLS does a sequential, exhaustive search for the best variable or combination of variables. Furthermore, it can be operated in "forward" mode, where intervals are successively included in the analysis, or in "reverse" mode, where intervals are successively removed from the analysis.
The "interval" in IPLS can be either a single variable or a "window" of adjacent variables (as might be used with spectroscopically-correlated or time-correlated variables, where adjacent variables are related to each other). In this discussion, we will refer to an "interval" with the understanding that this may include one ore more variables.
In forward mode, IPLS starts by creating individual PLS models, each using only one of the pre-defined variable intervals. This is similar to what is shown in GA Figure 1, except that only one of the individual intervals can be "on" at a time. If there are 100 intervals defined for a given data set, the first step calculates 100 models (one for each interval). Cross-validation is performed for each of these models and the interval which provides the lowest model root-mean-square error of cross-validation (RMSECV) is selected. This is the best single-interval model and the first selected interval, I1.
If only one interval is desired, the algorithm can stop at this point returning the one selected interval. If, however, more than one interval is desired (to increase information available to the model and maybe, thereby, improve performance), additional cycles can be performed. In the second cycle, the first selected interval is used in all models but is combined with each of the other remaining intervals, one at a time, when creating a new set of new PLS models. Again using RMSECV, the best combination of two intervals (I1 and one additional interval, I2) is determined. Note that the first selected interval can not change at this point. This is repeated for as many intervals as requested (up to In). Reverse mode of IPLS works in an opposite manner to forward mode. All intervals are initially included in the models, and the algorithm selects a single interval to discard. The interval which, when excluded, produced a model with the best RMSECV is selected for permanent exclusion. This is the "worst" interval, I1. If the user has selected that more than one interval should be excluded, subsequent cycles discard the next worst intervals based on improved RMSECV when each interval is discarded.
For more information on this method see the following paper:
L. Nergaard, A. Saudland, J. Wagner, J.P. Nielsen, L. Munck, and S.B. Engelsen, “Interval Partial Least-Squares Regression (iPLS): A Comparative Chemometric Study with an Example from Near-Infrared Spectroscopy” Applied Spectroscopy, 54 (3), 413-419, 2000
Practical IPLS Considerations
The total number of intervals to include or drop (number of cycles to perform) depends on various factors, including but not limited to:
- The expected complexity of the system being modeled – the more complex (e.g., non-linear) the data, the more intervals usually needed.
- The amount of data reduction necessary – if only a fixed number of variables can be measured in the final experiment, the number of intervals should be limited.
- The distribution of information in the variables – the more distributed the information, the more intervals needed for a good model.
One method to select the best number of intervals is to cross-validate by repeating the variable selection using different sub-sets of the data. There is no automatic implementation of this approach in PLS_Toolbox. However, the IPLS algorithm does allow one to indicate that the algorithm should continue to add (or remove) intervals until the RMSECV does not improve. This can give a rough estimate of the total number of useful intervals. If multiple runs with different sub-sets of the data are done using this feature, it can give an estimate of the likely "best" number of intervals.
Another consideration is interval "overlap". Variables in the data can be split in a number of ways.
- Intervals can each contain a single variable, thereby allowing single-variable selection.
- Intervals can contain a unique range or "window" of variables where each variable exists in only one interval.
- Intervals can contain overlapping ranges of variables where variables may be included in two or more intervals and can be included by selecting any of those intervals.
The decision on which approach to use depends on the uniqueness of information in the variables of the data and how complex their relationships are. If variables are unique in their information content, single-variable intervals may be the best approach. If adjacent variables contain correlated or complementary information, intervals which contain ranges of variables may provide improved signal-to-noise, increased speed of variable selection, and decreased chance of over-fitting (that is, selecting variables which work well on the calibration data but not necessarily on any data for the given system).
In contrast, although allowing overlapping intervals may seem as though it provides the advantages of increased signal-to-noise and modeling complexity, it may also lead to over-fitting. The difference between two adjacent windows becomes only the variables on the edges of the windows (those which are dropped or added by selecting the neighboring intervals.) In addition, overlapping windows can increase the analysis time considerably.
One general caveat to IPLS variable selection should be carefully considered. It is possible that, given n different intervals, the best "single interval" model would be obtained by selecting a given interval (interval 10, for example). The best "two interval" model, however, might actually be obtained by selecting two different intervals (5 and 6, for example). Because of the step-wise approach to this IPLS algorithm, once the single best interval is selected, it is required to be included in all additional models. As a result, the two-interval model might include intervals 5 and 10 (because 10 was selected first), even though 5 and 6 would provide a better RMSECV. This type of situation is most likely to arise when data are complex and require a significant number of factors for modeling. In these situations, using larger interval "windows" and requiring the addition of additional intervals (cycles) should be used. Additionally, the GA method of variable selection may provide superior results.
Using the IPLS Function
In Solo and PLS_Toolbox, the IPLS functionality is available in the Analysis Window for the analysis methods PLS, PLSDA, MLR, and PCR. Settings for the variable selection can be made from the IPLS Variable Selection Interface. Use of the settings on that interface are described on the linked page.
In PLS_Toolbox, the ipls function can be used at the command-line where it takes as input the X- and Y-block data to be analyzed, the size of the interval windows (1 = one variable per interval), the maximum number of latent variables to use in any model, and an options structure. The options structure allows selection of additional features including:
- mode : defines forward or reverse analysis mode.
- numintervals : defines the total number of intervals which should be selected. A value of inf tells IPLS to continue selecting until the RMSECV does not improve.
- stepsize : defines the number of variables between the center of each window. By default, this is empty, specifying that windows should abut each other but not overlap (i.e., stepsize is equal to the window size).
- mustuse : indices of variables which must be used in all models, whether or not they are included in the "selected" intervals.
- preprocessing : defines the preprocessing to be performed on each data subset (for more information, see the preprocess function).
- cvi : cross-validation settings to use (for more information, see the cvi input to the crossval function).
Demonstration of the ipls function can be done through the analysis of the slurry-fed ceramic melter (SFCM) thermocouple data. Briefly, these data consist of measurements from twenty thermocouples at various depths in a tank of melted ceramic material. As the level of the material rises and falls, the different thermocouples experience different temperatures. One can use IPLS to consider which thermocouple or thermocouples are the most useful in determining the level of material.
To do this, ipls is called with the SFCM data and inputs to set the maximum number of latent variables, interval width, and preprocessing options (autoscaling, in this case):
» load pls_data
» options = ipls('options');
» options.preprocessing = {'autoscale' 'autoscale'};
» int_width = 1; %one variable per interval
» maxlv = 5; %up to 5 latent variables allowed
» sel = ipls(xblock1,yblock1,int_width,maxlv,options);
The result is the plot shown in Figure 1.
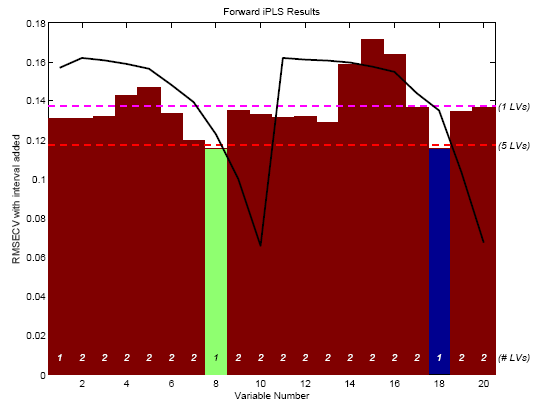
Figure 1. First selected interval for SFCM data.
The figure shows the RMSECV obtained for each interval (with the average sample superimposed as a black line). The numerical values inside the axes along the bottom (just above the variable number) indicate the number of latent variables (LVs) used to obtain the given RMSECV. Because each interval contains only a single variable, only 1 LV can be calculated in all cases. The green interval (variable 18) is the selected interval. The horizontal dashed lines indicate the RMSECV obtained when using all variables and 1 or 5 LVs. Note that interval 18 on its own gave a slightly better one-LV model than did the model using all twenty variables. However, a five-LV model using all variables still did better than any individual interval.
The commands below repeat this analysis but request that two intervals be selected instead of one. The plot shown in Figure 2 is the result.
» options.numintervals = 2; » sel = ipls(xblock1,yblock1,int_width,maxlv,options);
Figure 2. First two selected intervals for SFCM data.
The figure shows the results at the end of all interval selections. The final selected nth interval is shown in green. Intervals selected in the first n-1 steps of the algorithm are shown in blue. Because this analysis included only two intervals being selected, there is only one interval shown in blue (the first selected interval) and the second selected interval is shown in green. The height shown for the selected intervals (blue and green) is equal to the RMSECV for the final model. In this case, the final model with two selected intervals used only one latent variable (as indicated at the bottom of the bars) and gave an RMSECV which was slightly better than the RMSECV obtained using five latent variables and all intervals (dashed red line). Interestingly, the variables selected (numbers 8 and 18) are duplicate measurements at the same depth in the tank. This is a good indication that the given depth is a good place to measure, should only a single thermocouple be used.
The final example for IPLS shows the reverse analysis of the gasoline samples. In this case, the Y-block being predicted is the concentration of one of five components in these simulated gasoline mixtures and the X-block is the near-IR spectra measured for each sample. The reverse IPLS analysis indicates the effect on the RMSECV when each interval is discarded, and therefore the best interval(s) to discard. In this case, IPLS will be run with the maxintervals option set to infinity to trigger the "automatic" mode. The ipls function will continue to remove intervals until removing an interval would cause the RMSECV to increase. The MATLAB commands are shown below; the resulting plot is shown in Figure 3.
» load nir_data
» options = ipls('options');
» options.preprocessing = {'autoscale' 'autoscale'};
» options.numintervals = inf;
» ipls(spec1,conc(:,1),25,5,options);
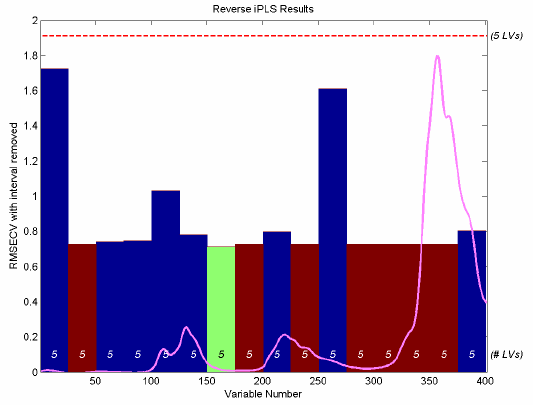
Figure 3. Reverse IPLS analysis for simulated gasoline samples.
A total of eight intervals were discarded before it was determined that removing any additional intervals would cause an increase in RMSECV. Intervals marked in red on the reverse IPLS results plot are those that were discarded in the first seven cycles. The interval marked in green was the last discarded interval. The blue intervals are those that were retained. Each bar indicates the RMSECV which would have resulted, had the given interval been discarded. It can be seen that the intervals centered at 38, 113, and 263 are all critical for a good model (discarding these intervals would result in a significant increase in RMSECV.) It can also be seen that intervals at 63 and 88 were likely candidates for exclusion in the last cycle as the RMSECV change would have been nearly negligible.
It is interesting to compare the IPLS results on the gasoline simulant shown in Figure 3 to those from the GA run on the same data, shown in GA Figure 7. Note that, with a few exceptions, the same regions are discarded in each case. The biggest discrepancy is the inclusion of the interval centered at variable 113. This interval was under-represented in the GA models, but appears to be highly important to the model formed with IPLS-based selection. The difference is likely due to IPLS having excluded some region in an earlier cycle which left the 113-centered interval as the only source of some information.
In contrast, the GA models discovered that a different combination of intervals could achieve a better RMSECV by discarding interval 113 and retaining a different interval. Note, incidentally, that the final model created by IPLS selection returns an RMSECV of around 0.71. This is in contrast with the GA result of 0.27 for the same data.
Conclusions
In general it should be remembered that, although variable selection may improve the error of prediction of a model, it can also inadvertently throw away useful redundancy in a model. Using a fewer number of variables to make a prediction means that each variable has a larger influence on the final prediction. If any of those variables becomes corrupt, there are fewer other variables to use in its place. Likewise, it is harder to detect a failure. If you keep only as many measured variables as you have latent variables in a model, you cannot calculate Q residuals, and the ability to detect outliers is virtually eliminated (except by considering T2 values). As such, the needs of the final model should always be carefully considered when doing variable selection.