Pca: Difference between revisions
imported>Chuck |
imported>Chuck No edit summary |
||
| Line 11: | Line 11: | ||
===Description=== | ===Description=== | ||
Performs a principal component analysis decomposition of the input array data returning ncomp principal components. E.g. for an ''M'' by ''N'' matrix '''X''' the PCA model is '''X''' = '''TP'''<sup>T</sup> + '''E''', where the scores matrix '''T''' is ''M'' by ''K'', the loadings matrix '''P''' is ''N'' by ''K'', the residuals matrix '''E''' is ''M'' by ''N'', and ''K'' is the number of factors or principal components ncomp. The output model is a PCA model structure. This model can be applied to new data by passing the model structure to PCA along with new data newdata or by using PCAPRO. The output of PCA is a model structure with the following fields (see MODELSTRUCT for additional information): | Performs a principal component analysis decomposition of the input array data returning ncomp principal components. E.g. for an ''M'' by ''N'' matrix '''X''' the PCA model is '''X''' = '''TP'''<sup>T</sup> + '''E''', where the scores matrix '''T''' is ''M'' by ''K'', the loadings matrix '''P''' is ''N'' by ''K'', the residuals matrix '''E''' is ''M'' by ''N'', and ''K'' is the number of factors or principal components ncomp. The output model is a PCA model structure. This model can be applied to new data by passing the model structure to PCA along with new data newdata or by using PCAPRO. | ||
PARAFAC (PARAllel FACtor analysis) for multi-way arrays | |||
===Synopsis=== | |||
:model = parafac(X,ncomp,''initval,options'') | |||
:pred = parafac(Xnew,model) | |||
===Description=== | |||
PARAFAC will decompose an array of order ''N'' (where ''N'' >= 3) into the summation over the outer product of ''N'' vectors (a low-rank model). E.g. if ''N''=3 then the array is size ''I'' by ''J'' by ''K''. An example of three-way fluorescence data is shown below.. | |||
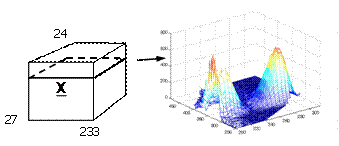
For example, twenty-seven samples containing different amounts of dissolved hydroquinone, tryptophan, phenylalanine, and dopa are measured spectrofluoremetrically using 233 emission wavelengths (250-482 nm) and 24 excitation wavelengths (200-315 nm each 5 nm). A typical sample is also shown. | |||
[[Image:Parafacdata.gif]] | |||
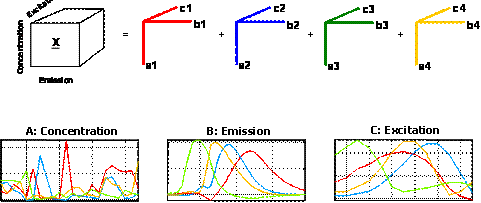
A four-component PARAFAC model of these data will give four factors, each corresponding to one of the chemical analytes. This is illustrated graphically below. The first mode scores (loadings in mode 1) in the matrix '''A''' (27x4) contain estimated relative concentrations of the four analytes in the 27 samples. The second mode loadings '''B''' (233x4) are estimated emission loadings and the third mode loadings '''C''' (24x4) are estimated excitation loadings. | |||
[[Image:Parafacresults.gif]] | |||
In the PARAFAC algorithm, any missing values must be set to NaN or Inf and are then automatically handled by expectation maximization. This routine employs an alternating least squares (ALS) algorithm in combination with a line search. For 3-way data, the initial estimate of the loadings is usually obtained from the tri-linear decomposition (TLD). | |||
====Inputs==== | |||
* '''x''' = the multiway array to be decomposed, and | |||
* '''ncomp''' = | |||
:* the number of factors (components) to use, OR | |||
:* a cell array of parameters such as {a,b,c} which will then be used as starting point for the model. The cell array must be the same length as the number of modes and element j contain the scores/loadings for that mode. If one cell element is empty, this mode is guessed based on the remaining modes. | |||
====Optional Inputs==== | |||
* '''''initval''''' = | |||
:* If a parafac model is input, the data are fit to this model where the loadings for the first mode (scores) are estimated. | |||
:* If the loadings are input (e.g. model.loads) these are used as starting values. | |||
*'''''options''''' = discussed below. | |||
====Outputs==== | |||
The output of PCA is a model structure with the following fields (see MODELSTRUCT for additional information): | |||
* '''modeltype''': 'PCA', | * '''modeltype''': 'PCA', | ||
Revision as of 11:51, 8 October 2008
Purpose
Perform principal components analysis.
Synopsis
- pca
- model = pca(x,ncomp,options); %identifies model (calibration step)
- pred = pca(x,model,options); %projects a new X-block onto existing model
Description
Performs a principal component analysis decomposition of the input array data returning ncomp principal components. E.g. for an M by N matrix X the PCA model is X = TPT + E, where the scores matrix T is M by K, the loadings matrix P is N by K, the residuals matrix E is M by N, and K is the number of factors or principal components ncomp. The output model is a PCA model structure. This model can be applied to new data by passing the model structure to PCA along with new data newdata or by using PCAPRO.
PARAFAC (PARAllel FACtor analysis) for multi-way arrays
Synopsis
- model = parafac(X,ncomp,initval,options)
- pred = parafac(Xnew,model)
Description
PARAFAC will decompose an array of order N (where N >= 3) into the summation over the outer product of N vectors (a low-rank model). E.g. if N=3 then the array is size I by J by K. An example of three-way fluorescence data is shown below..
For example, twenty-seven samples containing different amounts of dissolved hydroquinone, tryptophan, phenylalanine, and dopa are measured spectrofluoremetrically using 233 emission wavelengths (250-482 nm) and 24 excitation wavelengths (200-315 nm each 5 nm). A typical sample is also shown.
A four-component PARAFAC model of these data will give four factors, each corresponding to one of the chemical analytes. This is illustrated graphically below. The first mode scores (loadings in mode 1) in the matrix A (27x4) contain estimated relative concentrations of the four analytes in the 27 samples. The second mode loadings B (233x4) are estimated emission loadings and the third mode loadings C (24x4) are estimated excitation loadings.
In the PARAFAC algorithm, any missing values must be set to NaN or Inf and are then automatically handled by expectation maximization. This routine employs an alternating least squares (ALS) algorithm in combination with a line search. For 3-way data, the initial estimate of the loadings is usually obtained from the tri-linear decomposition (TLD).
Inputs
- x = the multiway array to be decomposed, and
- ncomp =
- the number of factors (components) to use, OR
- a cell array of parameters such as {a,b,c} which will then be used as starting point for the model. The cell array must be the same length as the number of modes and element j contain the scores/loadings for that mode. If one cell element is empty, this mode is guessed based on the remaining modes.
Optional Inputs
- initval =
- If a parafac model is input, the data are fit to this model where the loadings for the first mode (scores) are estimated.
- If the loadings are input (e.g. model.loads) these are used as starting values.
- options = discussed below.
Outputs
The output of PCA is a model structure with the following fields (see MODELSTRUCT for additional information):
- modeltype: 'PCA',
- datasource: structure array with information about input data,
- date: date of creation,
- time: time of creation,
- info: additional model information,
- loads: cell array with model loadings for each mode/dimension,
- pred: cell array with model predictions for the input block (when blockdetail='normal' x-block predictions are not saved and this will be an empty array)
- tsqs: cell array with T2 values for each mode,
- ssqresiduals: cell array with sum of squares residuals for each mode,
- description: cell array with text description of model, and
- detail: sub-structure with additional model details and results.
If the inputs are a Mnew by N matrix newdata and and a PCA model model, then PCA applies the model to the new data. Preprocessing included in model will be applied to newdata. The output pred is structure, similar to model, that contains the new scores, and other predictions for newdata.
Note: Calling pca with no inputs starts the graphical user interface (GUI) for this analysis method.
Options
options = a structure array with the following fields:
- display: [ 'off' | {'on'} ], governs level of display to command window,
- plots: [ 'none' | {'final'} ], governs level of plotting.
- outputversion: [ 2 | {3} ], governs output format (discussed below),
- algorithm: [ {'svd'} | 'maf' | 'robustpca' ], algorithm for decomposition,
- Algorithm 'maf' requires Eigenvector's MIA_Toolbox.
- preprocessing: {[]}, cell array containing a preprocessing structure (see PREPROCESS) defining preprocessing to use on the data (discussed below),
- blockdetails: [ {'standard'} | 'all' ], level of detail included in the model for predictions and residuals.
- confidencelimit: [ {'0.95'} ], confidence level for Q and T2 limits. A value of zero (0) disables calculation of confidencelimits.
- roptions: structure of options to pass to robpca (robust PCA engine from the Libra Toolbox).
- alpha: [ {0.75} ], (1-alpha) measures the number of outliers the algorithcarbuggym should resist. Any value between 0.5 and 1 may be specified. These options are only used when algorithm is 'robustpca'.
The default options can be retreived using: options = pca('options');.
OUTPUTVERSION
By default (options.outputversion = 3) the output of the function is a standard model structure model. If options.outputversion = 2, the output format is:
- [scores,loads,ssq,res,reslm,tsqlm,tsq] = pca(xblock1,2,options);
where the outputs are
- scores = x-block scores,
- loads = x-block loadings
- ssq = the sum of squares information,
- res = the Q residuals,
- reslim = the estimated 95Found limit line for Q residuals,
- tsqlim = the estimated 95Found limit line for T2, and
- tsq = the Hotelling's T2 values.
PREPROCESSING
The preprocessing field can be empty [] (indicating that no preprocessing of the data should be used), or it can contain a preprocessing structure output from the PREPROCESS function. For example options.preprocessing = {preprocess('default', 'autoscale')}. This information is echoed in the output model in the model.detail.preprocessing field and is used when applying the PCA model to new data.
See Also
analysis, evolvfa, ewfa, explode, parafac, plotloads, plotscores, preprocess, ssqtable