Mlr: Difference between revisions

Latest revision as of 07:52, 4 August 2022

Purpose

Multiple Linear Regression for multivariate Y.

Synopsis

model = mlr(x,y,options)

pred = mlr(x,model,options)

valid = mlr(x,y,model,options)

mlr % Launches analysis window with MLR as the selected method.

Please note that the recommended way to build and apply a MLR model from the command line is to use the Model Object. Please see this wiki page on building and applying models using the Model Object.

Description

MLR identifies models of the form Xb = y + e.

Inputs

x = X-block: predictor block (2-way array or DataSet Object)

y = Y-block: predictor block (2-way array or DataSet Object)

Outputs

model = scalar, estimate of filtered data.

pred = structure array with predictions

valid = structure array with predictions

Options

options = a structure array with the following fields.

display: [ {'off'} | 'on'] Governs screen display to command line.

plots: [ 'none' | {'final'} ] governs level of plotting.

algorithm: [ {'leastsquares'} | 'ridge' | 'ridge_hkb' | 'optimized_ridge' | 'optimized_lasso' | 'elasticnet' ] Governs the level of regularization used when calculating the regression vector.

condmax: [{[ ]}] Value for maximum condition number. Default value = [] leads to MLR calculation at full rank. Any value > 0 leads to truncation of factors based upon SVD until the condition number is less than the specified value. Used only for algorithm 'leastsquares'.

ridge: [ { 1 } ] Scalar value for ridge parameter for algorithm 'ridge'.

optimized_ridge: Vector of ridge (L2) entries used to determine optimized value for θ for algorithms 'optimized_ridge' or 'elasticnet'

optimized_lasso: Vector of ridge (L1) entries used to determine optimized value for θ for algorithms 'optimized_lasso' or 'elasticnet'

preprocessing: { [] [] } preprocessing structure (see PREPROCESS).

blockdetails: [ 'compact' | {'standard'} | 'all' ] level of detail (predictions, raw residuals, and calibration data) included in the model.

‘Standard’ = the predictions and raw residuals for the X-block as well as the X-block itself are not stored in the model to reduce its size in memory. Specifically, these fields in the model object are left empty: 'model.pred{1}', 'model.detail.res{1}', 'model.detail.data{1}'.
‘Compact’ = for this function, 'compact' is identical to 'standard'.
'All' = keep predictions, raw residuals for both X- & Y-blocks as well as the X- & Y-blocks themselves.

MLR Algorithms

Leastsquares

Standard MLR regression carried out to the full rank of the x-block is obtained by setting options.algorithm = 'leastsquares' and leaving options.condmax empty (default setting). For options.condmax > 0, singular value decomposition is performed on $X^{T}X$ , and factors are removed from the decomposition (in reverse order of the eigenvalues) until the condition number of the covariance matrix is less than this value.

Beginning with PLS_Toolbox/Solo 9.1, additional options are available for regularization when constructing MLR models. Adding regularization to an MLR model may be helpful when the x-block is ill-conditioned and can also be used as a variable selection tool.

Ridge

Ridge regularization based upon the standard formulation from Hoerl and Kennard (1970) $\beta =(X^{T}X+\theta I)^{-1}X^{T}Y$ may be selected by setting options.algorithm = 'ridge' and setting a positive scalar value for $\theta$ (regularization parameter) in options.ridge; the regression vector $\beta$ is calculated directly through matrix inversion.

Ridge HKB

An estimate of an optimal value for and the corresponding regression vector $\beta$ may be determined using the method of Hoerl, Kennard, and Baldwin (1975) by setting options.algorithm = 'ridge_hkb'. No other parameters are used for this option and the resulting optimal value of $\theta$ is calculated by matrix inversion.

Optimized Ridge

Ridge regularization can also be cast as an optimization (in this case, the L2 norm of $\beta$ ) and is included for completeness. For this case, options.algorithm = 'optimized_ridge' and the optimal value of $\theta$ is obtained from the range in options.optimized_ridge (vector). This mode may be used to place bounds around the value of $\theta$ .

Optimized Lasso

Lasso regularization minimizes the L1 norm of $\beta$ and uses the settings options.algorithm = 'optimized_lasso' and supplying a vector of values for the appropriate parameter in options.optimized_lasso.

Elasticnet

Elastic net regularization seeks to minimize the L2 and L1 norms of $\beta$ simultaneously using the initial estimates for the parameters in options.optimized_ridge and options.optimized_lasso, respectively. The appropriate value for options.algorithm is 'elasticnet' for this scenario.

The following figure shows the valid settings options.algorithm and the corresponding parameters which are used as inputs for these methods:

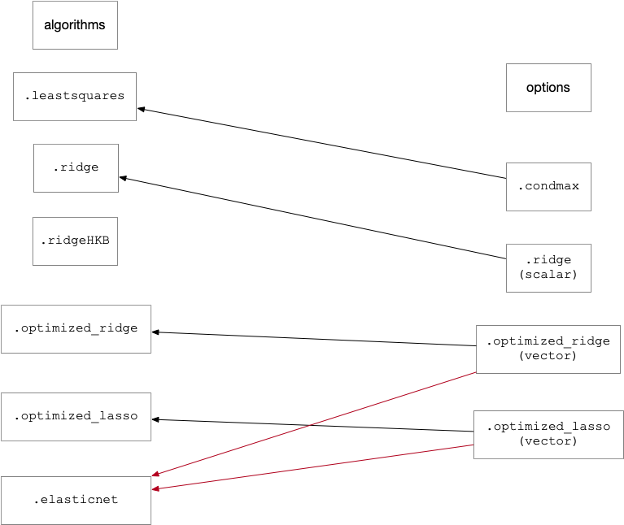
Note that the MATLAB Parallel Computing Toolbox (PCT) will be used for calculations based upon numerical optimization if installed, but is not required. Regression vectors are available for all algorithms from model.reg. The following table provides a list of parameters provided in the calibrated models specific to each algorithm:

algorithm	calibrated model parameters
`'leastsquares'`	`model.detail.mlr.condmax_value`: `condmax` (specified at model building) `model.detail.mlr.condmax_ncomp`: number of components used based upon `condmax`
`'ridge'`	$\theta$ : `model.detail.ridge_theta`
'`ridge_hkb'`	$\theta$ : `model.detail.mlr_ridge_hkb_theta`
`'optimized_ridge'`	`model.detail.mlr.optimized_ridge_theta` contains the vector of L2 ( $\theta$ ) values supplied in `options.optimized_ridge` `model.detail.mlr.best_params.optimized_ridge` contains the best single value for L2( $\theta$ ) from the values in `model.detail.mlr.optimized_ridge_theta`
`'optimized_lasso'`	`model.detail.mlr.optimized_lasso_theta` contains the vector of L1 ( $\theta$ ) values supplied in `options.optimized_lasso` `model.detail.mlr.best_params.optimized_lasso` contains the best single value for L1( $\theta$ ) from the values in `model.detail.mlr.optimized_lasso_theta`
`'elasticnet'`	entries above for both `optimized_ridge` and `optimized_lasso` algorithms apply

In MLR, our hypothesis function is

$h_{\beta }(x)=\beta ^{T}X$

where $\beta$ is the regression vector we wish to calculate.

The loss function for MLR is

$L(h_{\beta }(x_{i}),y)={\frac {1}{2}}(h_{\beta }(x_{i})-y_{i})^{2}.$

The cost function $J_{\beta }$ is used to minimize the loss $L(h_{\beta }(x_{i}),y)$ , and is found by the following equation

$J_{\beta }={\frac {1}{m}}\sum _{i=1}^{m}L(h_{\beta }(x_{i}),y)$

But when it comes to regularization, the $J_{\beta }$ is differed by the incorporation of the penalty terms. Consult the table below to note the differences in the cost functions between each algorithm:

options.algorithm	$J_{\beta }$ (Cost Function)
'leastsquares'	${\frac {1}{m}}\sum _{i=1}^{m}L(h_{\beta }(x_{i}),y)$
'optimized_ridge'	${\frac {1}{m}}\sum _{i=1}^{m}L(h_{\beta }(x_{i}),y)+{\frac {\theta _{a}}{2m}}\sum _{j=1}^{n}\beta _{j}^{2}$
'optimized_lasso'	${\frac {1}{m}}\sum _{i=1}^{m}L(h_{\beta }(x_{i}),y)+{\frac {\theta _{b}}{2m}}\sum _{j=1}^{n}\|\beta _{j}\|$
'elasticnet'	${\frac {1}{m}}\sum _{i=1}^{m}L(h_{\beta }(x_{i}),y)+{\frac {\theta _{b}}{2m}}\sum _{j=1}^{n}\|\beta _{j}\|+{\frac {\theta _{a}}{2m}}\sum _{j=1}^{n}\beta _{j}^{2}$

Note: $\theta _{a}$ pertains to the L2 penalty value and $\theta _{b}$ pertains to the L1 penalty value.

Studentized Residuals

From version 8.8 onwards, the Studentized Residuals shown for MLR Scores Plot are now calculated for calibration samples as:

 MSE   = sum((res).^2)./(m-1);
 syres = res./sqrt(MSE.*(1-L));

where res = y residual, m = number of samples, and L = sample leverage. This represents a constant multiplier change from how Studentized Residuals were previously calculated. For test datasets, where pres = predicted y residual, the semi-Studentized residuals are calculated as:

 MSE   = sum((res).^2)./(m-1);
 syres = pres./sqrt(MSE);

This represents a constant multiplier change from how the semi-Studentized Residuals were previously calculated.

@@ Line 18: / Line 18: @@
 ====Inputs====
-* '''y''' = X-block: predictor block (2-way array or DataSet Object)
+* '''x''' = X-block: predictor block (2-way array or DataSet Object)
 * '''y''' = Y-block: predictor block (2-way array or DataSet Object)
@@ Line 38: / Line 38: @@
 * '''plots''': [ 'none' | {'final'} ]  governs level of plotting.
-* '''algorithm''': [ {'leastsquares'} | 'ridge' | 'lasso' | 'elasticnet' ] Governs the level of regularization used when calculating the regression vector. 'ridge' uses the L2 penalty, 'lasso' uses the L1 penalty', and 'elasticnet' uses both L1 and L2.
+* '''algorithm''': [ {'leastsquares'} | 'ridge' | 'ridge_hkb' | 'optimized_ridge' | 'optimized_lasso' | 'elasticnet' ] Governs the level of regularization used when calculating the regression vector.
-* '''ridge''': [ 0 ] Value(s) for the ridge parameter to use in regularizing the inverse for ridge or elasticnet regression [ridge >=0 ].
+* '''condmax''': [{[ ]}] Value for maximum condition number. Default value = [] leads to MLR calculation at full rank. Any value > 0 leads to truncation of factors based upon SVD until the condition number is less than the specified value. Used only for algorithm 'leastsquares'.
-* '''lasso''': [   ] Value(s) for the lasso parameter to use in regularizing the inverse for lasso or elasticnet regression [lasso >=0 ].
+* '''ridge''': [ { 1 } ] Scalar value for ridge parameter for algorithm 'ridge'.
+* '''optimized_ridge''': Vector of ridge (L2) entries used to determine optimized value for θ for algorithms 'optimized_ridge' or 'elasticnet'
+* '''optimized_lasso''': Vector of ridge (L1) entries used to determine optimized value for θ for algorithms 'optimized_lasso' or 'elasticnet'
 * '''preprocessing''':  { [] [] } preprocessing structure (see PREPROCESS).
@@ Line 51: / Line 55: @@
 :* 'All' = keep predictions, raw residuals for both X- & Y-blocks as well as the X- & Y-blocks themselves.
-====MLR Regularization====
+====MLR Algorithms====
-Starting in PLS_Toolbox/Solo 9.1, we have added the ability to incorporate regularization when calculating the regression vector. Adding regularization to a Linear Regression model is known to reduce calibration overfitting. Ridge regularization was able to be performed before 9.1, but to a limited degree. MLR now can do Lasso and Elasticnet regularization in addition to Ridge. Ridge regression uses the L2 penalty as a part of minimizing the cost function, while Lasso uses the L1 penalty and Elasticnet uses a combination of both L1 & L2. You will see that the '''ridge''' and '''lasso''' fields in the method options structure contains an array of different values. What this means is that when using MLR with regularization is that each of these values in the ranges are tested in order to find the single best penalty value, creating the best corresponding regression vector. This is tested by doing a small random subset cross-validation on the calibration data, and the penalty that gives the best score from this cross-validation is to be noted as the best penalty. The best penalty/penalties can be found under '''model.detail.mlr.best_params''' (note that these will be empty if no regularization is used). In order to maximize speed in the model-building process, the Parallel Computing Toolbox (PCT) is used to do the model fitting between each of the penalty values. While PCT is nice to have, it is not required for MLR regularization.
+=====Leastsquares=====
+Standard MLR regression carried out to the full rank of the x-block is obtained by setting <code>options.algorithm = 'leastsquares'</code> and leaving <code>options.condmax</code> empty (default setting).  For options.condmax > 0, singular value decomposition is performed on <math>X^TX</math>, and factors are removed from the decomposition (in reverse order of the eigenvalues) until the condition number of the covariance matrix is less than this value.
+Beginning with PLS_Toolbox/Solo 9.1, additional options are available for regularization when constructing MLR models. Adding regularization to an MLR model may be helpful when the x-block is ill-conditioned and can also be used as a variable selection tool.
+=====Ridge=====
+Ridge regularization based upon the standard formulation from Hoerl and Kennard (1970)
+<math> \beta = (X^TX + \theta I)^{-1}X^TY</math>
+may be selected by setting <code>options.algorithm = 'ridge'</code> and setting a positive scalar value for <math>\theta</math> (regularization parameter) in <code>options.ridge</code>; the regression vector <math>\beta</math> is calculated directly through matrix inversion.
+=====Ridge HKB=====
+An estimate of an optimal value for  and the corresponding regression vector <math>\beta</math> may be determined using the method of Hoerl, Kennard, and Baldwin (1975) by setting <code>options.algorithm = 'ridge_hkb'</code>.  No other parameters are used for this option and the resulting optimal value of <math>\theta</math> is calculated by matrix inversion.
+=====Optimized Ridge=====
+Ridge regularization can also be cast as an optimization (in this case, the L2 norm of <math>\beta</math>) and is included for completeness.  For this case, <code>options.algorithm = 'optimized_ridge'</code> and the optimal value of <math>\theta</math> is obtained from the range in <code>options.optimized_ridge</code> (vector).  This mode may be used to place bounds around the value of <math>\theta</math>.
+=====Optimized Lasso=====
+Lasso regularization minimizes the L1 norm of <math>\beta</math> and uses the settings <code>options.algorithm = 'optimized_lasso'</code> and supplying a vector of values for the appropriate parameter in <code>options.optimized_lasso</code>.
+=====Elasticnet=====
+Elastic net regularization seeks to minimize the L2 and L1 norms of <math>\beta</math> simultaneously using the initial estimates for the parameters in <code>options.optimized_ridge</code> and <code>options.optimized_lasso</code>, respectively.  The appropriate value for <code>options.algorithm</code> is <code>'elasticnet'</code> for this scenario.
+The following figure shows the valid settings <code>options.algorithm</code> and the corresponding parameters which are used as inputs for these methods:
+[[File:MlrAlgorithmsOptions.png]]
+Note that the MATLAB Parallel Computing Toolbox (PCT) will be used for calculations based upon numerical optimization if installed, but is not required.
+Regression vectors  are available for all algorithms from <code>model.reg</code>.  The following table provides a list of parameters provided in the calibrated models specific to each algorithm:
+{| class="wikitable"
+! algorithm || calibrated model parameters
+|-
+| <code>'leastsquares'</code> || <code>model.detail.mlr.condmax_value</code>:
+<code>condmax</code> (specified at model building)
+<code>model.detail.mlr.condmax_ncomp</code>:
+number of components used based upon <code>condmax</code>
+|-
+| <code>'ridge'</code> || <math> \theta</math>: <code>model.detail.ridge_theta</code>
+|-
+| '<code>ridge_hkb'</code> || <math>\theta</math>: <code>model.detail.mlr_ridge_hkb_theta</code>
+|-
+| <code>'optimized_ridge'</code> || <code>model.detail.mlr.optimized_ridge_theta</code> contains the vector of L2 (<math>\theta</math>) values supplied in <code>options.optimized_ridge</code>
+<code>model.detail.mlr.best_params.optimized_ridge</code>
+contains the best single value for L2(<math>\theta</math>) from the values in
+<code>model.detail.mlr.optimized_ridge_theta</code>
+|-
+| <code>'optimized_lasso'</code> || <code>model.detail.mlr.optimized_lasso_theta</code> contains the vector of L1 (<math>\theta</math>) values supplied in <code>options.optimized_lasso</code>
+<code>model.detail.mlr.best_params.optimized_lasso</code>
+contains the best single value for L1(<math>\theta</math>) from the values in
+<code>model.detail.mlr.optimized_lasso_theta</code>
+|-
+| <code>'elasticnet'</code> || entries above for both <code>optimized_ridge</code> and <code>optimized_lasso</code> algorithms apply
+|}
 In MLR, our hypothesis function is
-<math> h_\theta(x) = \theta^{T}X </math>
+<math> h_\beta(x) = \beta^{T}X </math>
-where <math>\theta</math> is the regression vector we wish to calculate.
+where <math>\beta</math> is the regression vector we wish to calculate.
 The loss function for MLR is
-<math> L(h_\theta(x_i),y) = \frac{1}{2}(h_\theta(x_i) - y_i)^2. </math>
+<math> L(h_\beta(x_i),y) = \frac{1}{2}(h_\beta(x_i) - y_i)^2. </math>
-The cost function <math> J_\theta </math> is used to minimize the loss <math> L(h_\theta(x_i),y) </math>, and is found by the following equation
+The cost function <math> J_\beta </math> is used to minimize the loss <math> L(h_\beta(x_i),y) </math>, and is found by the following equation
-<math> J_\theta = \frac{1}{m} \sum^{m}_{i=1} L(h_\theta(x_i),y) </math>
+<math> J_\beta = \frac{1}{m} \sum^{m}_{i=1} L(h_\beta(x_i),y) </math>
-But when it comes to regularization, the <math> J_\theta </math> is differed by the incorporation of the penalty terms. Consult the table below to note the differences in the cost functions between each algorithm:
+But when it comes to regularization, the <math> J_\beta </math> is differed by the incorporation of the penalty terms. Consult the table below to note the differences in the cost functions between each algorithm:
 {| class="wikitable"
-! options.algorithm || <math> J_\theta </math> (Cost Function)
+! options.algorithm || <math> J_\beta </math> (Cost Function)
 |-
-| 'leastsquares' || <math> \frac{1}{m} \sum^{m}_{i=1} L(h_\theta(x_i),y) </math>
+| 'leastsquares' || <math> \frac{1}{m} \sum^{m}_{i=1} L(h_\beta(x_i),y) </math>
 |-
-| 'ridge' || <math> \frac{1}{m} \sum^{m}_{i=1} L(h_\theta(x_i),y)  + \frac{\lambda}{2m}\sum^{n}_{j=1}\theta_j^2</math>
+| 'optimized_ridge' || <math> \frac{1}{m} \sum^{m}_{i=1} L(h_\beta(x_i),y)  + \frac{\theta_a}{2m}\sum^{n}_{j=1}\beta_j^2</math>
 |-
-| 'lasso' || <math> \frac{1}{m} \sum^{m}_{i=1} L(h_\theta(x_i),y)  + \frac{\lambda}{2m}\sum^{n}_{j=1}|\theta_j|</math>
+| 'optimized_lasso' || <math> \frac{1}{m} \sum^{m}_{i=1} L(h_\beta(x_i),y)  + \frac{\theta_b}{2m}\sum^{n}_{j=1}|\beta_j|</math>
 |-
-| 'elasticnet' || <math> \frac{1}{m} \sum^{m}_{i=1} L(h_\theta(x_i),y)  + \frac{\lambda}{2m}\sum^{n}_{j=1}|\theta_j| + \frac{\lambda}{2m}\sum^{n}_{j=1}\theta_j^2</math>
+| 'elasticnet' || <math> \frac{1}{m} \sum^{m}_{i=1} L(h_\beta(x_i),y)  + \frac{\theta_b}{2m}\sum^{n}_{j=1}|\beta_j| + \frac{\theta_a}{2m}\sum^{n}_{j=1}\beta_j^2</math>
 |}
+Note: <math> \theta_a </math> pertains to the L2 penalty value and <math> \theta_b </math> pertains to the L1 penalty value.
 ====Studentized Residuals====

Mlr: Difference between revisions

Latest revision as of 07:52, 4 August 2022

Contents

Purpose

Synopsis

Description

Inputs

Outputs

Options

MLR Algorithms

Leastsquares

Ridge

Ridge HKB

Optimized Ridge

Optimized Lasso

Elasticnet

Studentized Residuals

See Also

Navigation menu

Mlr: Difference between revisions

Latest revision as of 07:52, 4 August 2022

Purpose

Synopsis

Description

Inputs

Outputs

Options

MLR Algorithms

Leastsquares

Ridge

Ridge HKB

Optimized Ridge

Optimized Lasso

Elasticnet

Studentized Residuals

See Also

Navigation menu

Search